课前，潘老师通过猜谜语的游戏提高学生的专注力。

“刚才我们提到了鸡和兔子，早在1500多年前的《孙子算经》里，就记载了一道和它们有关的趣题：‘今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？’” 

这句话用我们现在的话说就是：现在有一群鸡和兔子关在同一个笼子里，从上面数一共有35个头（鸡和兔各有一个头），从下面数一共有94只脚（鸡有2只脚，兔有4只脚），问鸡和兔子各有多少只？潘老师的解释让古老的数学题变得亲切易懂，孩子们的眼睛里闪着好奇的光。“不过今天我们先从一个更简单的问题入手——如果笼子里有8个头，26只脚，鸡和兔各有多少只呢？”

有的同学先在学习单上，从“鸡8只，兔0只”开始枚举可能的组合：

-当鸡8只、兔0只时，脚数=8×2+0×4=16只（比26少）；

-当鸡7只、兔1只时，脚数=7×2+1×4=18只（仍少）；

-当鸡6只、兔2只时，脚数=6×2+2×4=20只（少）；

-当鸡5只、兔3只时，脚数=5×2+3×4=22只（少）；

-当鸡4只、兔4只时，脚数=4×2+4×4=24只（少）；

-当鸡3只、兔5只时，脚数=3×2+5×4=6+20=26只（正好符合！）。

有的同学列到鸡0只时，更加完整。通过逐步调整鸡和兔的数量，同学们最终找到了正确答案：鸡3只，兔5只。

接着引导同学用“○”代表头，先画了8个○表示8个头。接着，他们给每个○先画2只脚（假设全是鸡），一共画了8×2=16只脚。但题目中总共有26只脚，还缺26-16=10只脚。于是，他们给部分“○”再添2只脚（每添2只脚，这个“○”就从鸡变成兔）。每添一次2只脚，脚数增加2只，需要添10÷2=5次。最终，有5个“○”是4只脚就是5只兔，剩下的8-5=3个“○”有2只脚，就是2只鸡。同理可以先画兔。

然后再到假设法：

假设全是鸡：总脚数应为8×2=16只，但实际有26只，少了26-16=10只脚。每只兔子比鸡多4-2=2只脚，所以兔子的数量=少的脚数÷每只兔多的脚数=10÷2=5只，鸡的数量=8-5=3只。

假设全是兔：总脚数应为8×4=32只，比实际多了32-26=6只脚。每只鸡比兔少4-2=2只脚，所以鸡的数量=多的脚数÷每只鸡少的脚数=6÷2=3只，兔子的数量=8-3=5只。

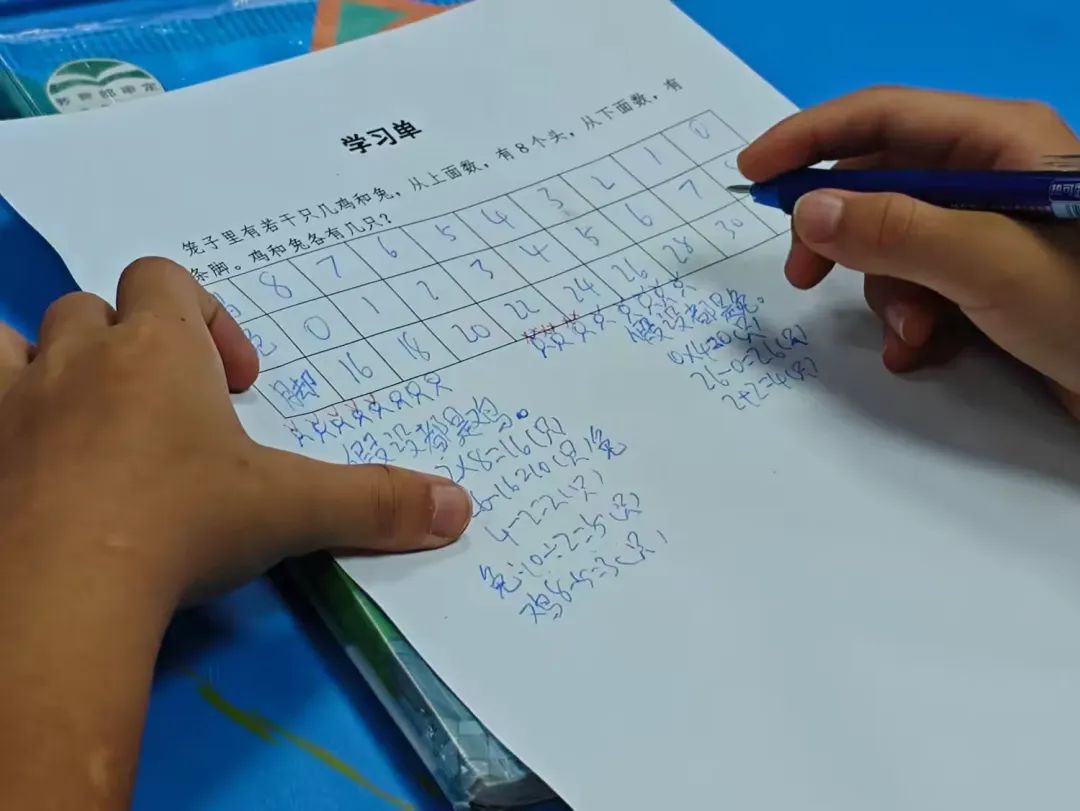
同学分享自己的做法，潘老师在讲解列表法与假设法的时候有运用智慧中小学平台给学生观看讲解。

韩诞平教导：鸡兔同笼问题，它的解决的方法有多种，潘老师从列表法开始讲解，然后通过画图的方法过渡，最后到假设法，我认为呢，应该是假设法是最好的，因为除了其他的其他的方法之外，假设法是最简便的，最容易让学生理解的一种方法，列表法和画图法，数小的时候还行，在数据大的时候就解决不了了，花的时间比较多。

郑芳老师：潘老师先把数据先变小了，小数据冲突的，然后接着调，也是列表法。然后教完画图法与列表法这两种方法之后，发现很麻烦，然后再把数据变大了，让学生来列表的话，他们觉得麻烦，有没有更好的，就想到了第三种假设法。但是假设法这里，然后你讲的这里不太透，少了十只脚，为什么？学生不太理解。

叶世辉组长：在利用智慧中小学平台讲讲列表法的时候，脚的只数为什么依次加2只，这样没有深挖，可以深挖为什么加2，为后面的假设法4-2=2做铺垫，还有画图有点小，可以画更大些，还有假设法还需要检验脚的数量。

黄宏海老师：画图法中多出来的10只脚和下面假设法中的全部假设是鸡26-16=10只是一样的，但是学生有些难理解，或者现在听懂了，做题又忘记了。